You should now Launch Deriver and do the 3 exercises of Predicate Exercise 7 (Predex7).
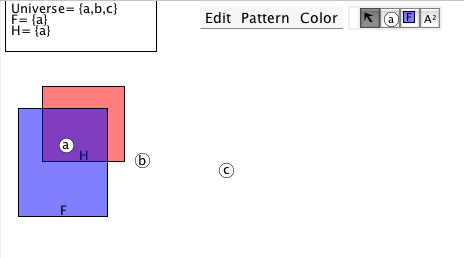
This will require some setting up. The Interpretation in Predex7 shows an Interpretation similar to this

and it certainly would be useful if your running Deriver also displayed this same Interpretation.
There are a few different workarounds to achieve the desired end:
Some of the following formulas contain 'free variables'. Such formulas do not have truth values as they stand (for their truth depends on which individuals the free variables represent).
Formulas with free variables gain a truth value once their free variables are valued. And there is a notation for this. As an example, the formula Fx has the free variable x and in this form it lacks a truth value, but say we decide to let x stand for the individual a, using the notation Fx[a/x], then the formula thus interpreted has a truth value (it actually is true in this diagram).
Another example, the formula Fx[c/x] is false in the diagram. The notation [a/x] is read "a for x" so the formula Fx[c/x] is read "F of x with c for x".
Form a view about the truth of each of the following formulas then ask
whether they are true (under the Semantics Menu).
a) (Ga∨Fb)∧Ha
b) (Ga∨Fb)∨Ha
c) Fx[a/x]
d) Fx[b/x]
e) Fx[c/x]
f) (Gy⊃Fb)[a/y]
d) ((Fz∧∼Gz)∧∼Hz)[a/z]
Form a view about the truth of each of the following formulas then ask whether they are true.
a) (∃x)Fx
b) (∃x)∼Fx
c) (∃x)Fx∧(∃x)∼Fx
d) (∃x)(Fx∧∼Fx)
e) (∀x)Fx
f) (∀x)(Hx⊃Fx) This formula symbolizes 'All H's are F.'; a common mistake is to symbolize 'All H's are F.' by means of the formula (∀x)(Hx∧Fx). Hence, see whether you think
g) (∀x)(Hx∧Fx)
is true.
Having mastered the use of '⊃' together with the Universal quantifier ∀ beginners often then proceed to make the second common mistake of using '⊃' with the Existential quantifier ∃.
h) (∃x)(Fx∧Gx)
This formula symbolizes 'Some F's are G' or, alternatively 'There is an F which is a G'. Consider whether it is true. Then go on to try its mistaken counterpart...
i) (∃x)(Fx⊃Gx)
j) A formula with the form (∀x)(Hx∧Fx) makes a very strong assertion, for it says 'Whatever x you choose, x is both H and F'.
Such assertions are hardly ever true. See if you can construct a formula like (∀x)(Hx∧Fx), or (∀x)(Gx∧Fx), or (∀x)(Hx∧Gx) ... which is true in the diagram.
k) On the other hand a formula with the form (∃x)(Fx⊃Gx) makes a very weak assertion, for it says 'There is an x such that if x is F then x is G' and this is the same as 'There is an x such that either x is not F or x is G'. Such assertions are hardly ever false.
See if you can construct a formula like (∃x)(Fx⊃Gx), or (∃x)(Fx⊃Hx), or (∃x)(Hx⊃Gx), ... which is false in the diagram.
Formulas may contain several quantifiers, for example
l) (∀x)(∀y)((Fx∧Gy)⊃∼Hx)
m) (∃x)(∃y)(Fx∧Hy)
What we have done so far can be generalized to lists of formulas. List of formulas are treated as though each of the components are joined together by conjunction ('∧')-- hence, a list true iff all components true, a list false iff at least one component false. Form a view about the truth of each of the following lists of formulas then ask whether they are true.
a) (∃x)Fx, (∃x)Gx,(∃x)Hx
b) (∃x)∼Fx,(∃x)∼Fx,(∃x)∼Hx
c) (∃x)(Fx∧Hx),(∃x)Gx
d) (∀x)(Hx⊃Fx),(∃x)Hx
e) (∀x)(Fx∨∼Fx),(∃y)(Fy∧Gy)
f) (∃x)(Fx∧Gx∧Hx),(∀x)(∼(Fx∧Gx∧Hx))
g) (∃x)(Fx⊃(Gx∨Hx)),(∀x)((Fx⊃∼(Gx∧Hx)))
h) (∀x)(∀y)((Fx∧Gy)⊃(Hx∧∼Hy)),(∃x)(∃y)(Fx∧Hy)