You should now Launch Deriver and do the 4 very important exercises of Predicate Exercise 14 (Predex14).
Show the Interpretation Panel
This uses the same interpretation as Predex13 and thus needs some setting up. The Interpretation in Predex14 shows an Interpretation similar to this

and it certainly would be useful if your running Deriver also displayed this same Interpretation.
There are a few workarounds to achieve the desired end:
The rule Universal Instantiation has the restriction on it that the proposed instantiation should not result in capturing (in the terminology... the variable of instantiation must be free for the term of instantiation in the scope).
So, for example,
(∀x)(∃y)Rxy ∴ (∃y)Ray
(∀x)(∃y)Rxy ∴ (∃y)Rby
(∀x)(∃y)Rxy ∴ (∃y)Rxy
(∀x)(∃y)Rxy ∴ (∃y)Rzy
are all valid arguments (and may be proved so by one use of Universal Instantiation). Derive them.
But
(∀x)(∃y)Rxy ∴ (∃y)Ryy
is invalid. Look at the interpretation of the diagram and note that all the premises are true and the conclusion false at one and the same time. This argument cannot be proved to be valid (for it is not). But the unwary might think that they can prove it by one use of Universal Instantiation which plugs in y (but this is the forbidden case where the y gets captured by the other quantifier).
The rule Universal Generalization has the restriction on it that the variable of quantification must not be free in the assumptions of the line on which it is used. The reason for this is that otherwise derivation of some invalid arguments would be possible.
Let us consider two arguments with free variables in the standing assumptions
a) Fx ∴ (∀y)Fx
and look at this semantically. Is is possible for all the premises to be true and the conclusion false at one and the same time?
Take the interpretation shown in the drawing
Universe= { a,b }
F= { a }
we cannot discuss the truth of Fx until we value its free variable and since we want it to be true we would try Fx[a/x] {ask for its truth} but under this valuation (∀y)Fx[a/x] is true also {ask}.
We might now suspect that the argument is valid, and indeed we can derive it (try it). Move on now to
b) Fx ∴ (∀x)Fx
Notice this time that the variable of quantification occurs free in the assumptions.
Look at this semantically. Is is possible for all the premises to be true and the conclusion false at one and the same time?
Take the interpretation shown in the drawing
Universe= { a,b }
F= { a }
we cannot discuss the truth of Fx until we value its free variable and since we want it to be true we would try Fx[a/x] {ask for its truth} but under this valuation (∀x)Fx[a/x] is false {ask}.
This means that the argument is invalid! The interpretation andvaluation prove it to be so. (Try doing a derivation if you wish.)
Arguments with free variables in their standing assumptions are relatively rare. But the rule for Existential Instantiation nearly always introduces a free variable into the current assumptions, because you take its scope as a new assumption and this will nearly always contain the variable that was used with the Existential Quantifier. So, if you start an Existential Instantiation and then use Universal Generalization, be careful.
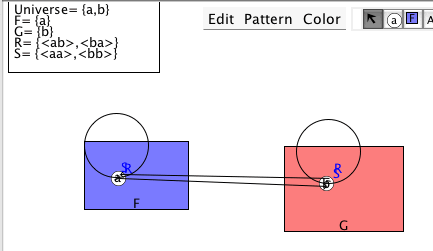
The rule Existential Generalization has the restriction on it that no occurrence of the term that you are generalizing on is bound by another quantifier. In other words, working back from the result back substitution should not result in capturing (in the terminology... the variable of generalization must be free for the term of generalization in the scope).
So, for example,
(∀x)Sxa ∴ (∃y)(∀x)Sxy
(∀x)Sxb ∴ (∃y)(∀x)Sxy
(∀x)Sxy ∴ (∃y)(∀x)Sxy
(∀x)Sxz ∴ (∃y)(∀x)Sxy
are all valid arguments (and may be proved so by one use of Existential Generalization). Derive them.
But
(∀x)Sxx ∴ (∃y)(∀x)Sxy
is invalid. Look at the interpretation of the diagram and note that all the premises are true and the conclusion false at one and the same time. This argument cannot be proved to be valid (for it is not). But the unwary might think that they can prove it by one use of Existential Generalization which generalizes on one occurrence of x (but this is the forbidden case where the occurrence is already quantified by another quantifier-- back substituting the x leads to it getting captured by the other quantifier).
The rule Existential Instantiation has on it two restrictions.
First the variable of instantiation must not occur free in the proposed
target instantiation. Consider the following argument.
(∃x)Fx∴Fx
It is invalid. To see this we have to value the free x in the
conclusion. Thus
(∃x)Fx∴Fx[b/x]
In the diagram, this has true premises and a false conclusion (check it). The first restriction on the EI rule stops invalid arguments, like the example, from being derived. Roughly speaking what is going on here is that the premise tells us at least one thing is F, and the conclusion tells us that x is F, but x is a free variable which might name anything in the Universe, and there are valuations in which at least one thing is F but x does not name any of them.
The second restriction on the EI rule is that the variable of instantiation must not occur free in the assumptions of the intended target.
Consider the argument.
Gx, (∃x)Fx∴(∃x)(Fx∧Gx)
It is invalid. To see this we have to value the free x in the premises.
Thus
Gx[b/x], (∃x)Fx∴(∃x)(Fx∧Gx)
In the diagram, this has true premises and a false conclusion(check it).
The second restriction on the EI rule stops invalid arguments, like the example, from being derived. Roughly speaking what is going on here is that one premise tells us at least one thing is F, and the other premise tells us that x is G, but x is a free variable which might name anything in the Universe, and there are valuations in which at least one thing is F but the x which is G does not name any of them (sure there is an F, sure there is a G, but there is no guarantee that something is both F and G).