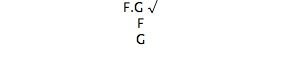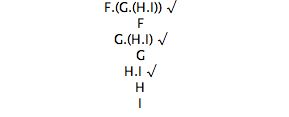1/27/08 10Software
Prerequisities
You need to know some sentential logic to be able to understand this. In particular, you need to know about the symbols used in sentential logic, truth tables, satisfiability, consistency, and semantic invalidity (by counter example). You do not need to know sentential rules of inference and derivations. [The tutorials on sentential logic give the required background.]
Skills to be acquired in this tutorial:
To become familiar with the notions of tree, branch, open branch, closed branch.
Reading
A. Hausman, H.Kahane, P.Tidman, [2007] Logic and Philosophy Chapter 6
[The use of trees (or 'tableaux') in logic was pioneered by Beth, Hintikka, and Smullyan, and their use was brought into a teaching context by such books as the standard Jeffrey text. See
E.W. Beth, [1959] The Foundations of Mathematics
G.Gentzen, [1934-5] 'Untersuchungen uber das logische Schliessen', Mathematische Zeitschrift, vol 39, 1934-5, pp.176-210, 405-31
J. Hintikka [1955] ' Two papers on Symbolic Logic', Acta Philosophica Fennica, vol 8 1955
R.C.Jeffrey, [1967] Formal Logic: Its Scope and Limits
R.M. Smullyan, [1968] First Order Logic
]
Tutorial:
Graph theory and trees
'Trees' are a type of structure within the mathematical theory of graphs.
Graphs consist of two things: nodes (other words for these, 'vertices', 'points') and links (other words for these, 'edges', 'lines', 'ties'). In applications, nodes typically model individual people, countries, businesses, web pages, genes, amino acids, etc. Links typically model friendships, web hyperlinks, telephone lines, communications, etc. For us, nodes are going to represent formulas and the links will show the decomposition, or transformation, of a formula into other formulas.
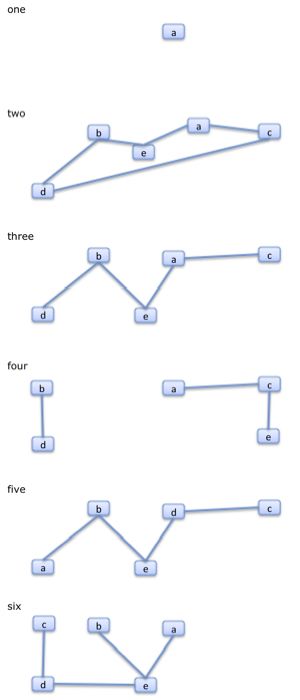
You can think of a node and being a dot or a point, and a link as being a line or an edge which runs from a node to a node. So here are a few graphs
The size of a graph is the number of nodes in it. Graph 1 is a graph consisting of a single node only. Graphs 2 and 5 are graphs with five nodes. Graph 3 has five nodes and four links; graph 5 also has five nodes and four links, but it is a different graph to 3 because different nodes are linked.
The degree of a node is the number of links that connect to it. So, for example, in Graph 6 above, three of the nodes have degree 1 but node d has degree 2 and e degree 4.
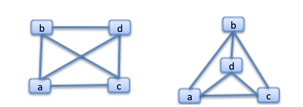
How the links are drawn is irrelevant (you can draw them as curves or straight lines or locate them differently, and the links can cross each other without that meaning anything)-- all that matters is which nodes they connect. These two graphs are actually the same graph.
A walk is an alternating sequence of nodes and links, which starts and ends with a node. So, in graph 2, a->e->b is a walk. A path is a walk with no repeated nodes. The length of a walk is the number of links included in it. Two nodes are adjacent if there is a link between them.
A graph has a cycle, or is cyclic, if there is a walk of non-zero length that starts and ends on the same node (otherwise the graph is said to be acyclic).
A graph is connected if there is a path between every two nodes in it. Graphs 2, 3, 5, and 6 are connected. Graphs 1 and 4 are not.
There are a couple of different ways of explaining or defining trees (and which is preferable depends a little on what is going to be done with the resulting trees).
A tree is a connected graph in which between every two nodes there is only one path (ie there are no 'cycles'). For example,
is a tree (you can walk from node to node (so it is connected) but you cannot walk around in a circle (so there are no cycles)).
The following is not a tree
because there is a cycle.
And the following is not a tree
because it is not connected.
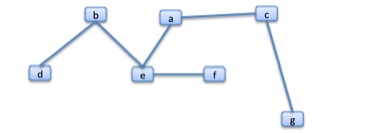
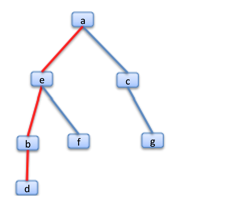
With the kind of trees of interest to us, it is usual to pick one of a tree's nodes as being the 'root'. Then it is common to draw them with the root at the top, and the other nodes appearing below. So if the node 'a' were to be chosen as the root of the real tree in the first diagram, the tree might be re-drawn.
You can imagine this re-drawing process as being that of picking up the root and shaking the whole tree so that the other nodes fall below. [The reason trees are often drawn 'upside down', with the root at the top, and the 'branches' and 'leaves' coming downward is that they are often constructed from the root and enough room has to be left on the sheet of paper to draw them.]
In computer science, there often is not a whole lot of interest as to which node is the root (and so, for example, there are algorithms to 'balance' trees and these amount to manipulating trees and their roots to produce an even result).
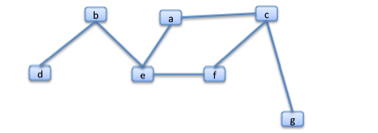
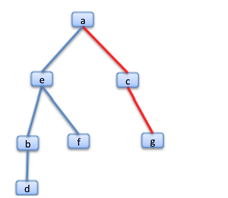
In our work, we almost always are going to be interested in which node is the root. So there will be a designated root. And, with a tree, there are nodes which do not have other nodes below them. These are leaves. So, in the above tree, 'a' is the root, and d, f and g are leaves. With any leaf, there is exactly one path from the root to it, such a path is a branch.
The red lines indicate the three branches in the above tree.
Truth Tree Rules
Trees are going to be used to 'picture' the truth conditions or requirements for a formula (then, as the technique is developed, for several formulas at once).
Any easy way to remember the rules is to regard them as having been built from the truth tables.
For example, the truth table for 'and' is
Conjunction
F G (F.G) True True True True False False False True False False False False
For a conjunction to be true, each of its immediate subformulas have to be true. A tree is started with the conjunction as the root, and it is extended by adding a branch containing each of the immediate subformulas. Thus
before
after
[These images come from the running applet that we will look at shortly, the tick is just to show which formula has been extended.]
The tree extension rules are also used to grow a tree even when the formula that is being used to make the extension is not the root. For example, here is a perfectly good tree built using the conjunction rule three times in a row (first on the root, then on one of the products of the first extension, and so on).
Try building some 'and' trees (click on the formula to select, choose 'extend' from the menu).
A tree 'pictures' truth conditions. It shows what has to happen for a formula to be true. The idea is: if all the atomic formulas in a branch are true, or are assigned true, and all the negations of atomic formulas in a branch are true, ie their atomic components are assigned false, then all the formulas in the branch will be true. So, for example, (F.G) is true if F is true and G is true, and (H.~I) is true if H is true and I is false. However, this is subject to a condition. Consider the formula (F.~F), it is not satisfiable, no assignment of truth values to its atomic components can make it true. If you do a tree for a formula like this (Tree 3 above), you will end up with a branch that has both F and ~F in it; this means that you will be trying to assign F both true and false (which is impossible).
Any branch that contains a formula and the negation of that formula is said to be closed. (And any branch that is not closed is open.)
The running applet allows you to close (suitable) branches. To do this you have to select two formulas (on WIndows and Mac computers this is done by clicking on the first then command-clicking on the second), one of the formulas has to be the negation of the other, then you select 'Close' from the menu.
A Note on Notation
The actual Hausman book uses a slightly different notation for justifying the lines in a tree. For example, it uses 'p' (for premise) for the opening lines, whereas the system here uses 'SM' (for set member).
Exercises to accompany Tutorial 1
Exercise 1 (of 1) (very brief):
For Tree 3 above, extend the tree, then select both F and ~F (click on the first, command click on the second) then select 'Close' from the menu. This is just to introduce you to the notation for closed branches.